Розмір кола доводиться визначати в задачах різного рівня. Щоб обчислення були точними, варто розуміти, як пов’язані між собою радіус, довжина та діаметр, тому що саме ця величина допомагає швидко знаходити потрібні параметри фігури без зайвих дій.
Основи вимірювання діаметра кола
Просте пояснення принципів дозволяє вільно працювати як з навчальними, так і з прикладними задачами. Спершу потрібно усвідомити, що діаметр кола це максимальна відстань між двома протилежними точками фігури, яка проходить через центр.
У геометрії зручно опиратися на властивість, за якою діаметр кола дорівнює двом радіусам, бо вона дає можливість швидко отримати один параметр, знаючи інший. Під час вимірювань іноді виникає потреба з'ясувати, який діаметр має коло, коли є лише приблизний зовнішній розмір предмета.
У задачах з формулами також доводиться розуміти, чому дорівнює діаметр, якщо задано площу круга або радіус, тому зв’язок між величинами важливо проговорити окремо.
Обчислення діаметра за відомою довжиною
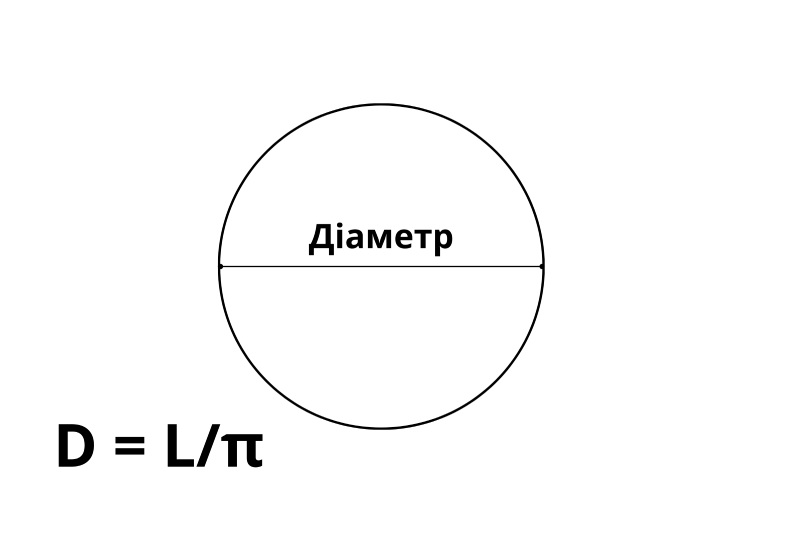
Під час розрахунків насамперед важливо розуміти, як визначити діаметр кола маючи довжину, адже формула довжини кола напряму пов’язана з діаметром: L = πD.
Звідси можна вивести вираз: D = L/π.
Завдяки цьому підходу легко розв’язати побутову задачу або перевірити результат у робочих кресленнях. Такий самий принцип застосовують у випадках, коли треба з’ясувати, як визначити діаметр кола за його довжиною, наприклад, під час розрахунку параметрів труб, дисків чи отворів. У багатьох збірниках задач трапляється формулювання, як знайти діаметр кола якщо відома довжина, і в кожній з них розв’язання спирається на цю ж формулу, тільки з іншими числами.
Щоб закріпити принцип, доречно подати кілька числових прикладів у стислому вигляді.
| Довжина кола (см) | Формула | Обчислення | Діаметр (см) |
|---|---|---|---|
| 31,4 | D = L / π | 31,4 ÷ 3,14 = 10 | 10 |
| 47,1 | D = L / π | 47,1 ÷ 3,14 = 15 | 15 |
| 62,8 | D = L / π | 62,8 ÷ 3,14 = 20 | 20 |
Протяжність як змінна у задачах
У задачах інколи потрібно з’ясувати, як визначити діаметр кола знаючи його протяжність, і тоді під словом “протяжність” розуміють довжину окружності. У такому випадку обчислення виконують через формулу L = πD, тому що між цими величинами існує пряма залежність. Якщо ж у задачі дано радіус, доводиться користуватися іншим співвідношенням – D = 2r. Формула змінюється залежно від того, яке значення подане в умові.
Короткий приклад для самоперевірки
Якщо довжина кола дорівнює 18,84 см, спочатку записують загальну формулу зв’язку довжини та діаметра: L = πD.
Далі потрібно виразити діаметр: D = L / π.
Після цього підставляють відомі значення: D = 18,84 / 3,14.
Виконують ділення 18,84 на 3,14 і отримують результат: D = 6,00 см.
Отже, для кола з довжиною 18,84 см діаметр дорівнює 6 см, і цей приклад наочно показує роботу формули при точних числових значеннях.
Обчислення для молодших школярів
На початковому рівні геометрії вчителі пояснюють, як знайти діаметр кола 3 клас, за допомогою простих кроків і наочних рисунків. Учні бачать, що діаметр проходить через центр і завжди більший за радіус рівно у два рази. Для перших вправ достатньо кількох вправ із уже накресленими колами та підписаними точками.
Алгоритм дій зручно подавати так:
- знайти центр;
- провести діаметр;
- позначити кінці;
- виміряти відстань;
- записати результат;
- перевірити вимір.
Приклад:
На рисунку накреслено коло з радіусом 4 см. Учень вимірює відстань від центра до будь-якої точки на колі й отримує 4 см. Щоб знайти діаметр, треба використати залежність D = 2r.
Підстановка значення: D = 2 × 4.
Отриманий результат: D = 8 см.
Такий приклад показує, що діаметр удвічі більший за радіус і легко знаходиться за найпростішою дією множення.
Приклади використання в реальних умовах
Під час роботи з великими або незручними для вимірювання предметами потрібно чітко розуміти, як визначити діаметр кола, коли не виходить прикласти лінійку просто поперек фігури. Наприклад, це стосується кришок, отворів у стінах, декоративних елементів або спортивного інвентарю, де зручніше виміряти гнучкою стрічкою саме довжину кола. Після цього діаметр легко обчислити за вже знайомою формулою L/π. У технічних сферах подібний підхід застосовують для перевірки деталей, які не можна розмістити на звичайній вимірювальній лінійці, але можна обхопити вимірювальною стрічкою чи шнуром.
У побуті ця навичка допомагає підбирати відповідні кришки, кільця, рамки або інші круглі елементи до вже наявних предметів. Варто один раз уважно пройти шлях від вимірювання довжини до розрахунку діаметра, щоб надалі застосовувати його автоматично.

Всі дії спираються на кілька простих співвідношень між радіусом, довжиною та діаметром. Коли формули стають звичними, обчислення перетворюються на коротку послідовність кроків, яку легко виконати в зошиті, на виробництві чи вдома.





